目录
目录连续系统时域分析解微分方程求响应零状态和零输入冲激和阶跃离散系统时域分析解差分方程求响应总结连续系统频域分析小知识点傅里叶级数函数正交分解原理傅里叶级数频率分量判断指数型傅里叶级数傅里叶变换傅里叶变换的推导傅里叶变换的复数特性傅里叶变换性质傅里叶变换对称性和反傅氏变换的运用希尔伯特变换-Hilbert Transform周期函数的傅里叶变换关于共轭对称性时域抽样与频域抽样连续系统S域分析Laplace变换Laplace变换性质单边拉氏变换和双边拉氏变换的区别Laplace逆变换离散系统Z变换Z变换求零输入响应三大变换关系拉氏变换到傅氏变换Z变换与拉氏傅氏变换双边拉氏变换和Z变换系统函数直接化简梅森增益公式稳定性分析系统零极点分析状态方程系统函数到状态方程电路到状态方程微分/差分方程到状态方程一些要点零散知识点系统的输入与响应附录#1_信号三大变换助记#2_梅森公式概念题
连续系统时域分析
解微分方程求响应
零状态和零输入
一个微分方程描述的系统:
可以得到关于
关于参数:
其中
冲激和阶跃
以下情况:
有以下解法:
其中求
阶跃响应同理,或用冲激响应求:
离散系统时域分析
解差分方程求响应
如以下差分方程:
零输入和零状态:
求零输入响应即求齐次解,和微分方程类似,但基本因子由
Tip:一般求全解会给出
冲激和阶跃响应:
冲激和阶跃序列再
利用
冲激响应求的是零状态响应,但冲激可看作注入状态。
求出齐次解,然后以
阶跃响应可设特解为常数,代入方程求特解:
冲激与阶跃序列的关系:
总结
求
冲激响应列齐次方程,求参数代入
连续系统频域分析
小知识点
正交函数集:利用不同函数积的积分为0,函数自乘的积分不为0的性质验证。
帕塞瓦尔定理:时域能量等于频域能量;能量:
帕塞瓦尔等式(常用于三角式或傅里叶级数形式信号算功率):
帕塞瓦尔方程/能量方程(计算题常见):
傅里叶级数
函数正交分解原理
将函数
以上,得到傅里叶系数,系数与正交基相乘求和得到傅里叶级数:
傅里叶级数频率分量判断
首先剔除直流项
奇函数只含
项,偶函数只含 项; 奇谐只含奇数项,偶谐只含偶数项;
以上3种搭配;
奇谐和偶谐:移动半周期重合为偶谐,移动半周期取反重合为奇谐;
指数型傅里叶级数
指数型傅里叶级数可以理解为两个来源:
将函数以复指数函数集展开,得到的就是指数型傅里叶级数;
将三角函数型傅里叶级数中的同频
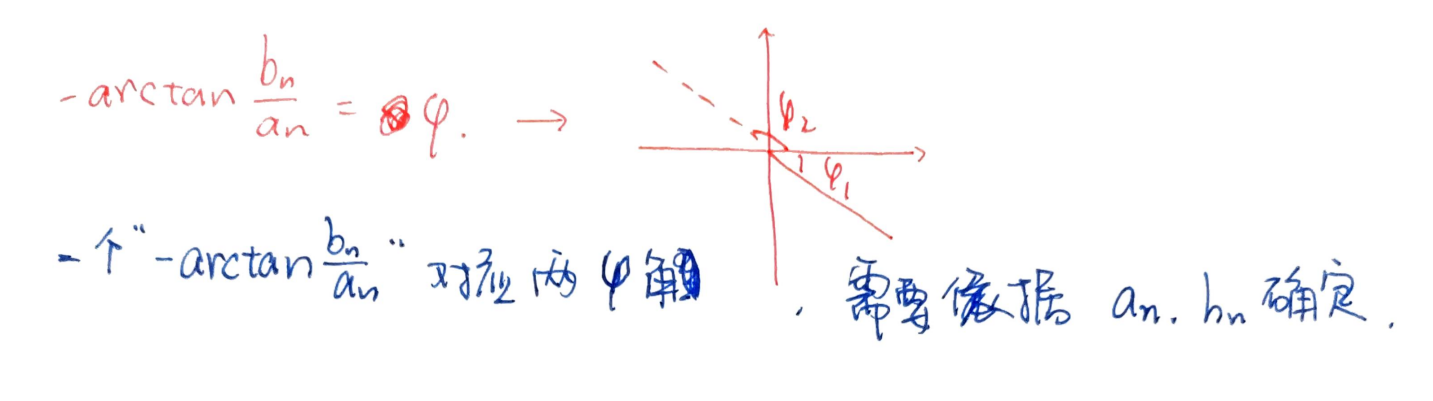
指数型傅里叶级数可以画出图像,即一个双边幅频谱和相频谱。关于相角
由于范围不同,所以由公式计算的结果需要通过
傅里叶变换
傅里叶变换的推导
对于指数型傅里叶级数:
周期拉长到
傅里叶变换的复数特性
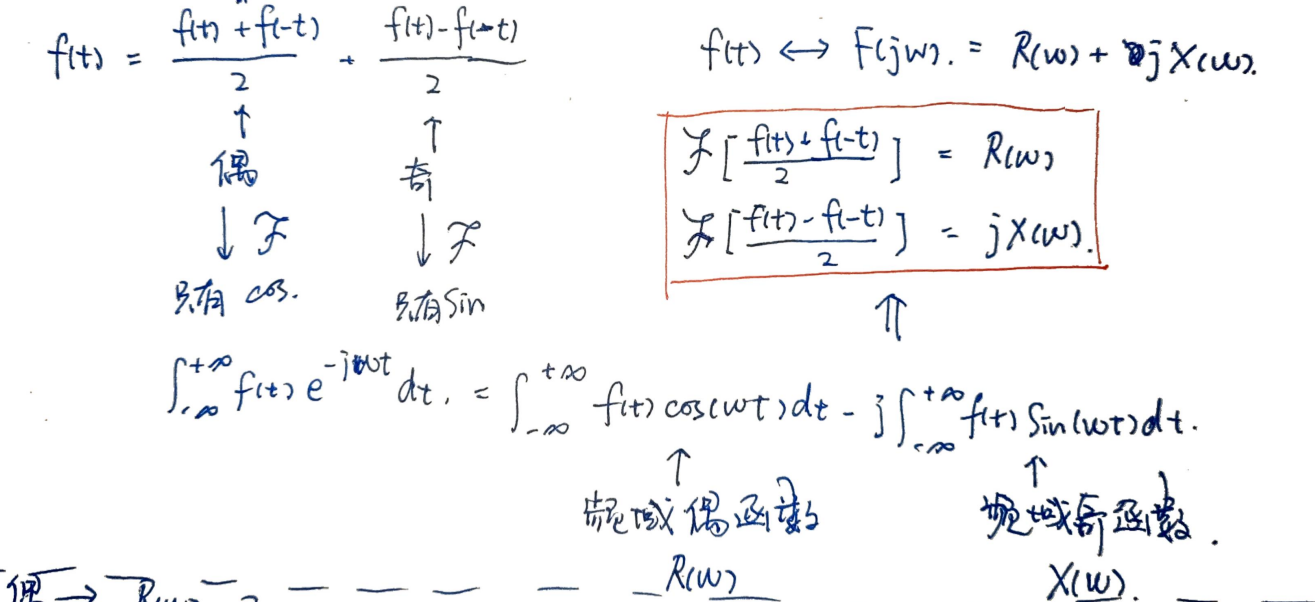
傅里叶变换后的复数形式理解:
理解如下:
Q1:傅氏变换后的实部和虚部有啥意义? 傅氏变换的思想就来自于高等数学里面的三角级数展开,高等数学里面的级数展开理论是:对于有限区间上的有限信号,都可以展开成以一系列不同正弦和余弦函数的叠加(就是用不同频率的正余弦信号分量叠加就得到了该原始信号)。傅氏变换后得到的复数,实部就代表该频率下的余弦信号分量,虚部就代表该频率下的正弦信号分量。
Q2:复数的模和相位有啥意义? 傅氏变换后得到的复数的模就是该频率下对应的正弦信号的振幅和余弦信号的振幅的绝对值的平方在开根。相位的意义就是该模乘以这个相位角的余弦值就得到了该频率下的余弦信号的振幅,乘以正弦值就得到了该频率下的正弦信号的振幅。
解释如下:

即
傅里叶变换性质
线性奇偶不讲;
;
,时域展宽,幅频压缩;
时域
频域乘 ,频域 时域乘 ; 时域微分频域乘
,频域微分时域乘 ; 积分初值
倍函数零点冲激; 时域卷积频域乘;
PS
通过性质可以助记常用傅里叶变换对:
基本变换对:
| 时域 | 频域 |
|---|---|
| 1 | |
PS:
傅里叶变换对称性和反傅氏变换的运用
傅里叶变换的对称性:
关于该性质的运用,本质是两个函数形式的寻找,即
确定题目中的函数形式,是
通过将
希尔伯特变换-Hilbert Transform
有一系统,其特性为:
则易知该系统为一移相器,正频率移相
同时有希尔伯特反变换:
即一个正频率移相
性质
正交变换,由于
因果信号的傅里叶变换实部与虚部构成希尔伯特变换对。
周期函数的傅里叶变换
对于周期函数:
其中
关于共轭对称性
什么是实函数:实函数即不带复数的函数,或只将实数映射为实数的函数(不严谨表述);
什么是函数的共轭:比较超纲,不谈。
共轭对称性的公式描述:
如果
共轭的东西有个特性,两者相乘等于模平方即:
时域抽样与频域抽样
时域抽样,频域周期延拓,频域抽样,时域周期延拓
连续系统S域分析
Laplace变换
S域与频域的区别
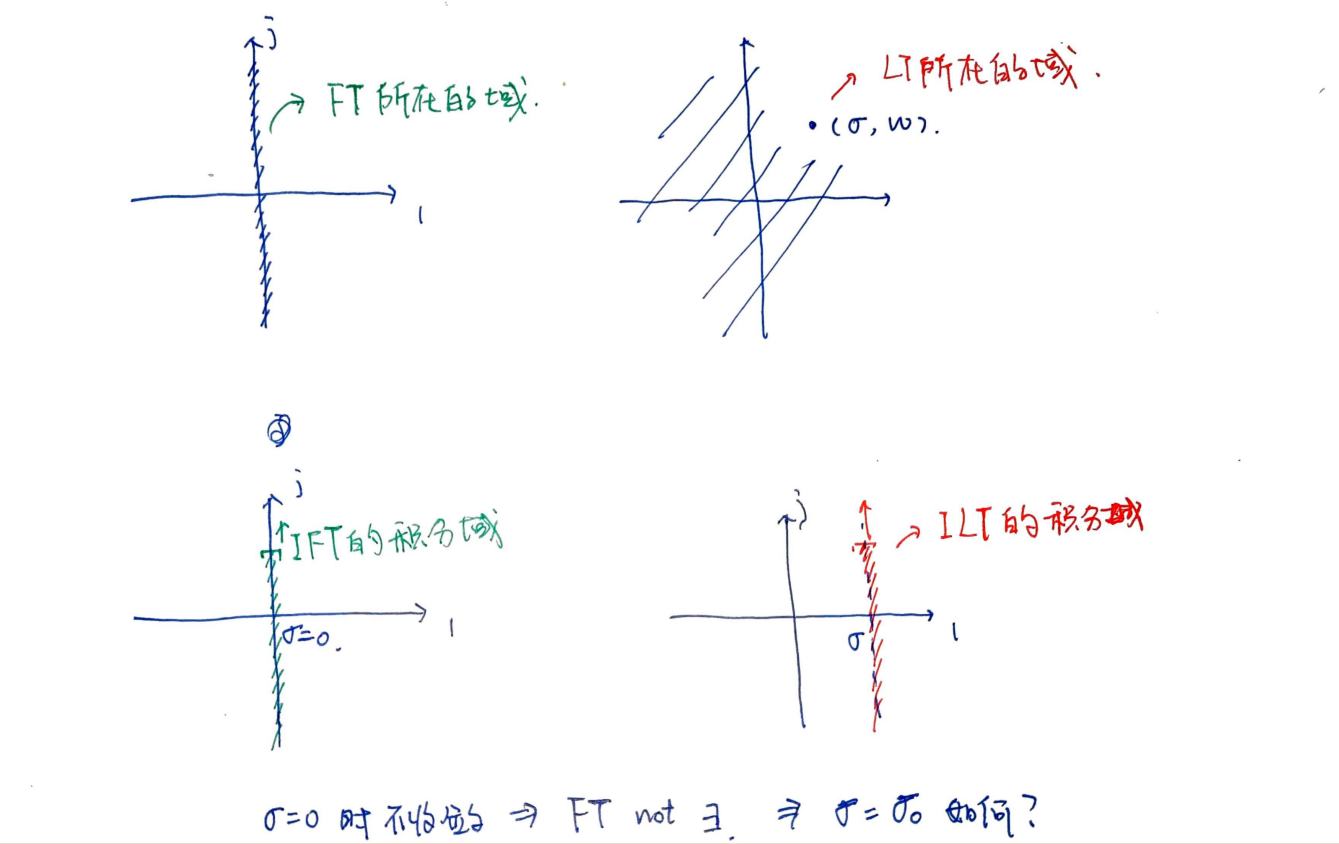
单边和双边拉普拉斯变换
双边:
单边:
反变换一致:
Laplace变换性质
同
| 注 | ||
|---|---|---|
| 时移收敛域不变,频移收敛域移动 | ||
| 时域微分频域乘 | 时域微分频域乘 | |
| 时域卷积频域乘; | 时域卷积同,无s域卷积 | |
| 积分初值 | 时域积分s域除 | |
| s域不对称 | ||
| 初值终值定理 | ||
单边拉氏变换和双边拉氏变换的区别
Laplace逆变换
一个像函数形式如下:
其中
极点全为单实根;
极点含共轭单根;
极点含重实根;
极点含复重根;
首先是最基本的因式分解法:
法一:常用于直接解实根
共轭复根
共轭复根的逆变换导出式:
N重根
有n重实根就将重根和单根分离,重根的部分将重根依次降阶写成n个分式:
复重根同理。其中,
公式分三部分:阶乘,求导和基本的乘极点,逆变换则需要使用到:
离散系统Z变换
对
单边z变换:
ROC的解释:
由于
; 不考虑
,首先虚轴经变换将蜷缩为一个圆,半径大小由 中的 决定,所以最后是个喇叭形;
Z变换求零输入响应
z变换求零状态响应直接求即可,但是遇到要求零输入响应或者全响应的情况,只能用单边z变换。即:
即对不该有的那一段求z变换,该加上加上,该减掉减掉;
记忆:
三大变换关系
拉氏变换到傅氏变换
首先看象函数在虚轴收不收敛
收敛,直接
不收敛,无频响函数
临界收敛,因式分解,将虚轴上的极点分离,转回时域再傅里叶变换,(如果是多个非重根)可得到:
如果是重根,那么根据思路直接推;
Z变换与拉氏傅氏变换
从Z变换可以求频率响应:
从z变换到拉普拉斯变换:
双边拉氏变换和Z变换
由双边拉氏变换表易知,同一象函数的双边逆变换即单边逆变换的表达式对
双边Z变换与拉氏相似,同一象函数的双边逆变换即单边逆变换的表达式对
系统函数
直接化简
如图,直接将支路按照串并联规则化简,最后消除自环;
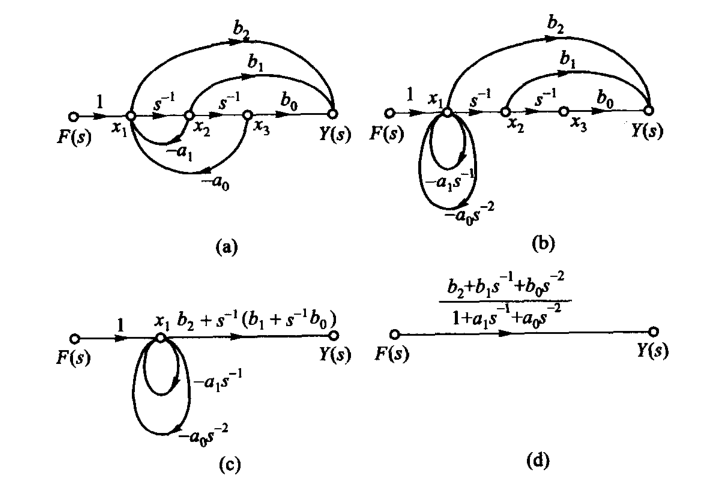
梅森增益公式
分母为
[注意]
前向通路:信号输入,顺着箭头走,每个节点只经过一次,到达输出的通路;
子图的行列式:某个前向通路的子图就是,将该前向通路连线带点拿掉,余下的图;然后对这个图求特征行列式;
环路:即字面意思;
依次可由
PS:一个
稳定性分析
一般直接极点全负判断就行,如果算不出所有极点,则:
如果
还是不行,用判据,如下:
罗斯阵列 - 时域判断
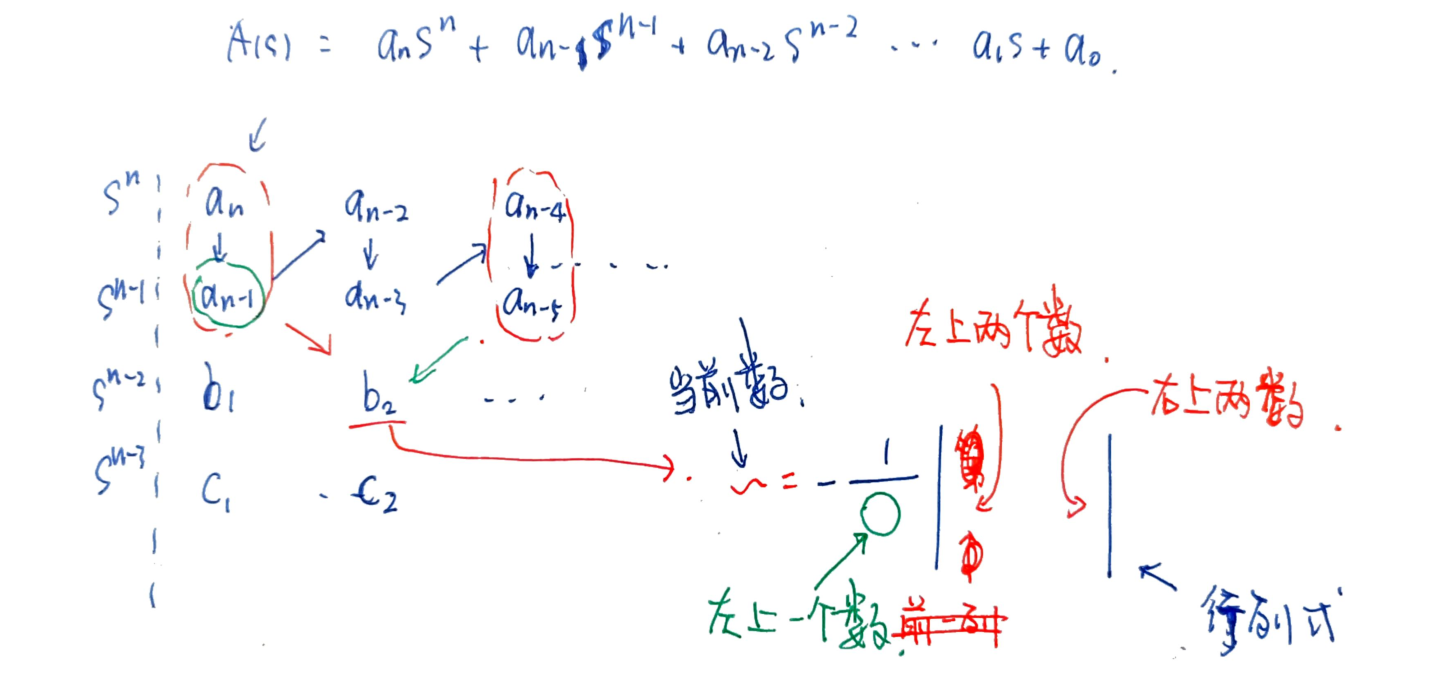
注意点
如果遇到0,当作无穷小继续算;
如果一行全是0,拿上一行作系数写
结论:第一列有正又有负,则不稳定
朱里准则 - 离散判断
不搞,作以下变换将罗斯判据判极点是否小于0映射为极点是否在单位圆内:
因果:
系统零极点分析
系统零极点对系统的影响:
系统零极点与信号
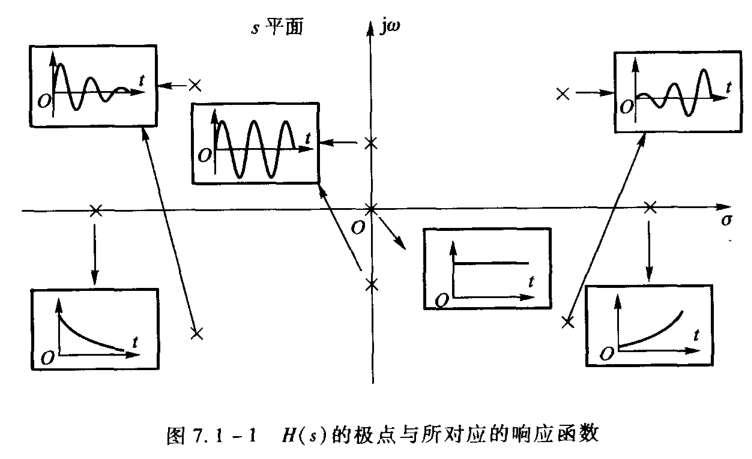
零极点与幅频相频响应
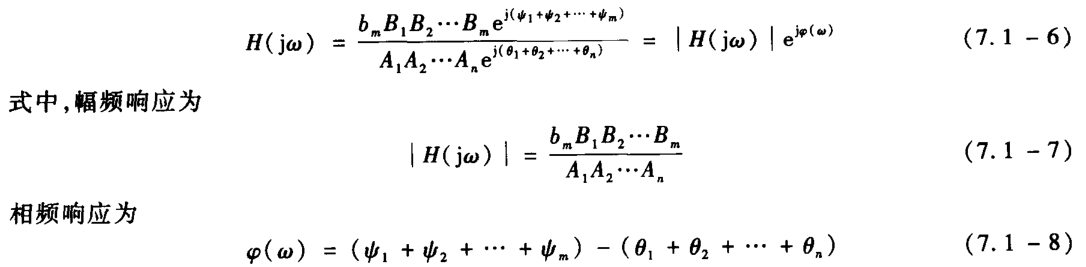
极点,零点与幅频
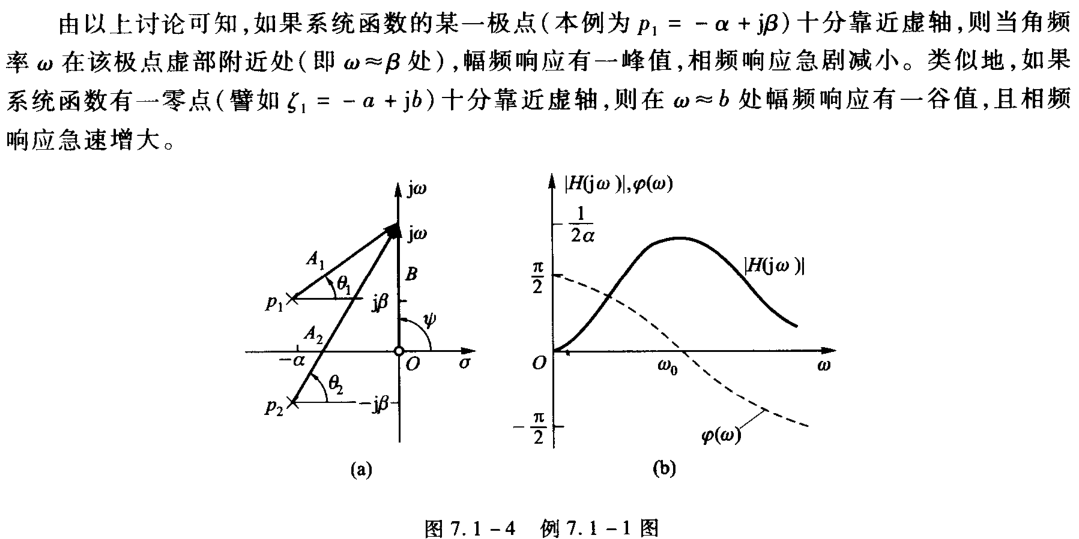
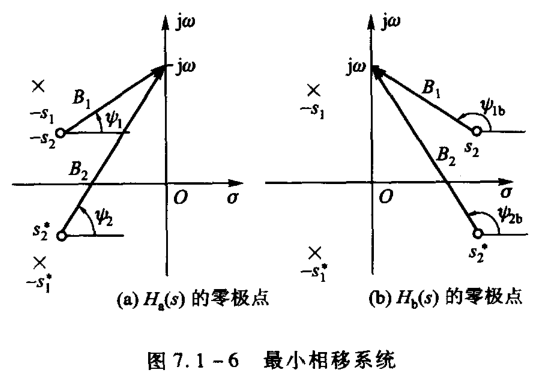
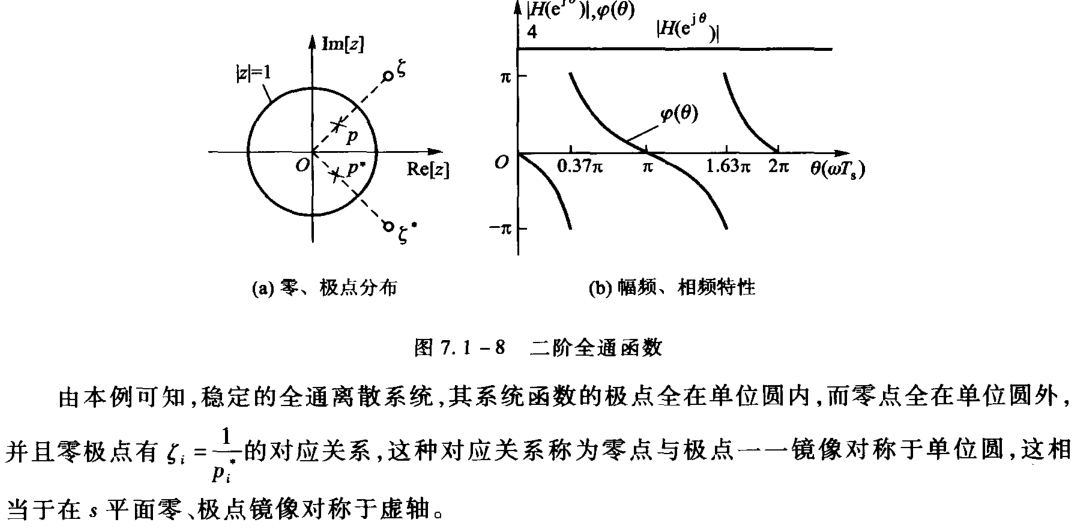
全通系统,最小相移系统,零极点与相频


状态方程
系统函数到状态方程

电路到状态方程
取独立动态元件的特性电气参数
解电路,将
微分/差分方程到状态方程

一些要点
零散知识点
系统的判定:
线性:
时不变:
信号的时移,反折,伸缩都是对于单个
拉氏变换带共轭复根时普通方法分离实根,式子减掉实部分后再将复根凑成三角型
时变判断只改
系统零极点到系统函数需要补上一个
系统的输入与响应
| 响应 | 描述 |
|---|---|
| 零输入响应 | 只含齐次解,初始状态产生的响应 |
| 零状态响应 | 含齐次解和特解,输入信号产生响应 |
| 自由相应 | 只含齐次解且齐次解就是自由响应,由系统本身(齐次形式)决定 |
| 强迫响应 | 只含特解且特解就是强迫响应,由输入信号形式(如指数型,三角型...)决定 |
| 暂态响应 | 逐渐衰减的响应 |
| 稳态响应 | 保持稳定的响应 |
[注]
系统的极点由系统本身决定,即特征方程的解;系统的零点由输入信号决定;
其中,系统初始状态可以决定一些参数
附录
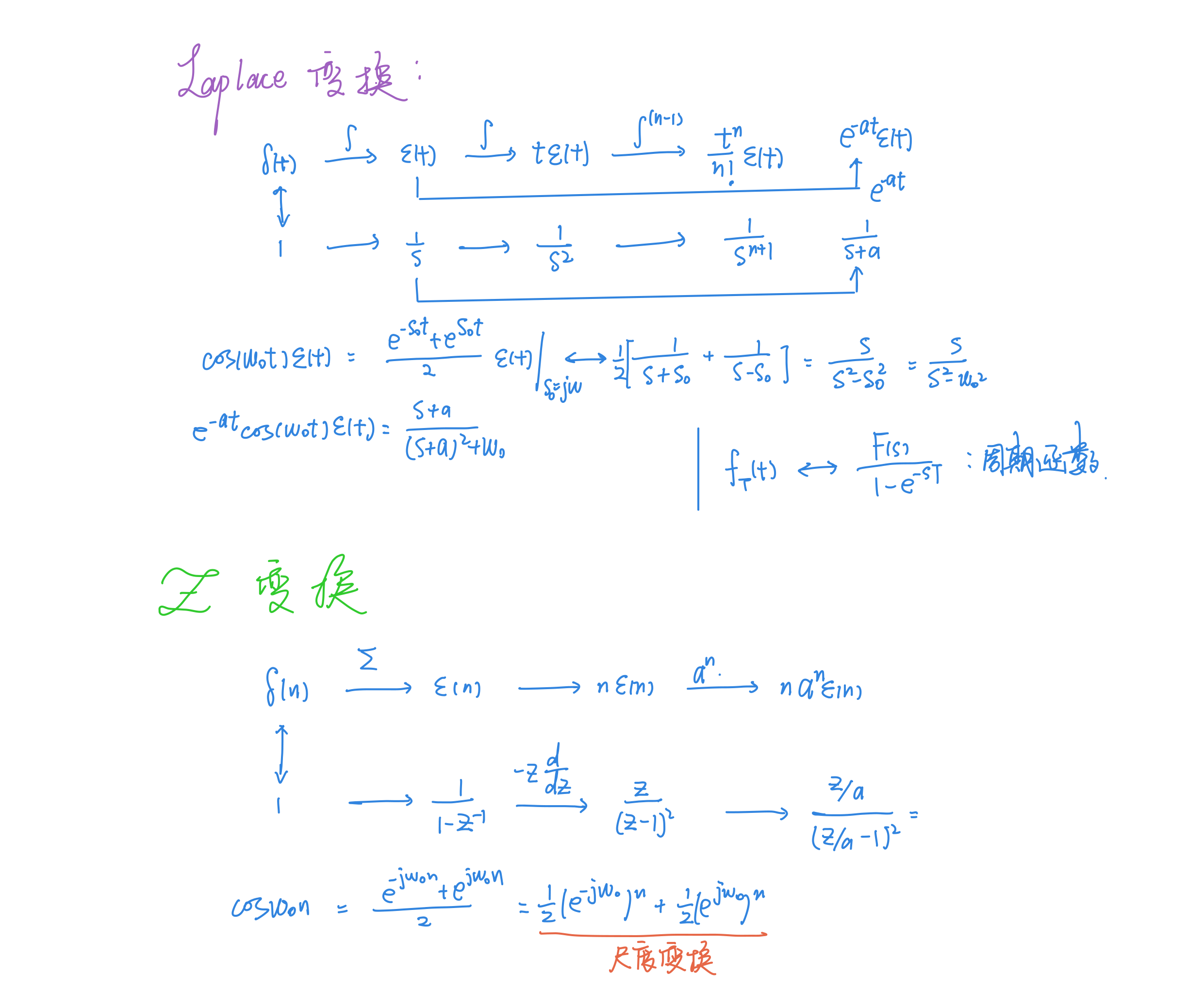
#1_信号三大变换助记

[注意] 其中Z变换移位中写的是双边z变换的移位性质,单边是:
即对不该有的那一段求z变换,该加上加上,该减掉减掉;
#2_梅森公式概念题